Sparse VAR on a Real Public Dataset, Herold et al. (2020)

In this example, we are goint to import the metabolite data and do a sparse VAR inference method to infer the causal relationships between the variables (relative abundances and metabolite concentrations) in the time series dataset available at Herold et al., 2020.

First, we will import the neccessary libraries and load the dataset.

[2]:

import matplotlib.pyplot as plt
import numpy as np


import pandas as pd
import seaborn as sns


from mimic.data_imputation.impute_GP import GPImputer
from mimic.model_infer.infer_VAR_bayes import *

WARNING:tensorflow:From c:\ProgramData\anaconda3\envs\MIMIC\Lib\site-packages\tf_keras\src\losses.py:2976: The name tf.losses.sparse_softmax_cross_entropy is deprecated. Please use tf.compat.v1.losses.sparse_softmax_cross_entropy instead.

WARNING:tensorflow:From c:\ProgramData\anaconda3\envs\MIMIC\Lib\site-packages\tensorflow_probability\python\internal\backend\numpy\_utils.py:48: The name tf.logging.TaskLevelStatusMessage is deprecated. Please use tf.compat.v1.logging.TaskLevelStatusMessage instead.

WARNING:tensorflow:From c:\ProgramData\anaconda3\envs\MIMIC\Lib\site-packages\tensorflow_probability\python\internal\backend\numpy\_utils.py:48: The name tf.control_flow_v2_enabled is deprecated. Please use tf.compat.v1.control_flow_v2_enabled instead.


WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.

So now, let’s try doing the inference with the VAR method and the imputed data to see if it can infer the causal relationships between the variables in the time series.

[3]:

imputed_data = pd.read_csv('imputed_data.csv')
# create a pandas dataframe of the original imputed data_set with days as the index
imputed_data.set_index('days', inplace=True)

[4]:

imputed_MP_data = pd.read_csv('MP_metabolite_imputed_data.csv')
imputed_MP_data.set_index('date', inplace=True)

imputed_MP_data.head(15)

[4]:
01_Fermentation 02_Homoacetogenesis 03_Superpathway of thiosulfate metabolism (Desulfovibrio sulfodismutans) 04_Utililization of sugar, conversion of pentose to EMP pathway intermediates 05_Fatty acid oxidation 06_Amino acid utilization biosynthesis metabolism 07_Nucleic acid metabolism 08_Hydrocarbon degradation 09_Carbohydrate Active enzyme - CAZy 10_TCA cycle ... 12_Transporters 13_Hydrogen metabolism 14_Methanogenesis 15_Methylotrophy 16_Embden Meyerhof-Parnos (EMP) 17_Gluconeogenesis 18_Sulfur compounds metabolism 19_Saccharide and derivated synthesis 20_Hydrolysis of polymers 21_Cellular response to stress
date
0.0 0.096899 0.009890 0.000579 0.000535 0.025483 0.122784 0.119531 0.005524 0.003921 0.045398 ... 0.015593 0.000846 0.003520 0.009267 0.030473 0.016261 0.005346 0.009267 0.006193 0.037334
1.0 0.104379 0.010097 0.000564 0.001093 0.026447 0.125917 0.111970 0.004937 0.003630 0.046199 ... 0.015868 0.000653 0.003944 0.011636 0.030150 0.016665 0.004634 0.008585 0.006081 0.036379
2.0 0.107954 0.010104 0.000564 0.001093 0.027555 0.125917 0.111924 0.004942 0.003630 0.046254 ... 0.015999 0.000653 0.003976 0.011727 0.030150 0.016687 0.004626 0.008435 0.006079 0.036373
3.0 0.110575 0.010110 0.000564 0.001093 0.028627 0.125917 0.111895 0.004947 0.003630 0.046306 ... 0.016125 0.000653 0.004017 0.011795 0.030150 0.016703 0.004616 0.008353 0.006077 0.036378
4.0 0.112957 0.010117 0.000564 0.001093 0.029633 0.125917 0.111872 0.004952 0.003630 0.046364 ... 0.016263 0.000653 0.004060 0.011858 0.030150 0.016720 0.004606 0.008309 0.006075 0.036393
5.0 0.115460 0.010125 0.000564 0.001093 0.030625 0.125917 0.111851 0.004957 0.003630 0.046434 ... 0.016427 0.000653 0.004105 0.011927 0.030150 0.016741 0.004598 0.008297 0.006072 0.036419
6.0 0.118505 0.010138 0.000564 0.001093 0.031655 0.125917 0.111830 0.004962 0.003630 0.046530 ... 0.016638 0.000653 0.004150 0.012011 0.030150 0.016773 0.004591 0.008324 0.006070 0.036465
7.0 0.123112 0.010161 0.000564 0.001093 0.032694 0.125917 0.111804 0.004966 0.003630 0.046688 ... 0.016966 0.000653 0.004197 0.012141 0.030150 0.016836 0.004588 0.008426 0.006067 0.036559
8.0 0.133734 0.011645 0.000340 0.000870 0.033575 0.129235 0.108779 0.004688 0.003063 0.052367 ... 0.018224 0.001059 0.004159 0.016334 0.035428 0.018678 0.003592 0.009150 0.006692 0.042688
9.0 0.123435 0.010154 0.000564 0.001093 0.033030 0.125917 0.111790 0.004976 0.003630 0.046701 ... 0.017093 0.000653 0.004302 0.012159 0.030150 0.016790 0.004592 0.008234 0.006062 0.036497
10.0 0.119160 0.010124 0.000564 0.001093 0.032334 0.125917 0.111801 0.004981 0.003630 0.046557 ... 0.016899 0.000653 0.004362 0.012048 0.030150 0.016679 0.004598 0.007934 0.006060 0.036339
11.0 0.116464 0.010103 0.000564 0.001093 0.031667 0.125917 0.111808 0.004986 0.003630 0.046478 ... 0.016835 0.000653 0.004425 0.011984 0.030150 0.016595 0.004602 0.007689 0.006057 0.036223
12.0 0.114334 0.010085 0.000564 0.001093 0.031067 0.125917 0.111815 0.004991 0.003630 0.046428 ... 0.016847 0.000653 0.004486 0.011937 0.030150 0.016514 0.004603 0.007452 0.006054 0.036115
13.0 0.112345 0.010067 0.000564 0.001093 0.030503 0.125917 0.111825 0.004997 0.003630 0.046399 ... 0.016938 0.000653 0.004540 0.011898 0.030150 0.016423 0.004597 0.007184 0.006051 0.035997
14.0 0.110036 0.010043 0.000564 0.001093 0.029966 0.125917 0.111846 0.005002 0.003630 0.046398 ... 0.017176 0.000653 0.004575 0.011857 0.030150 0.016293 0.004580 0.006819 0.006048 0.035833

15 rows × 21 columns

[5]:

imputed_MT_data = pd.read_csv('MT_metabolite_imputed_data.csv')
imputed_MT_data.set_index('date', inplace=True)

imputed_MT_data.head(15)

[5]:
01_Fermentation 02_Homoacetogenesis 03_Superpathway of thiosulfate metabolism (Desulfovibrio sulfodismutans) 04_Utililization of sugar, conversion of pentose to EMP pathway intermediates 05_Fatty acid oxidation 06_Amino acid utilization biosynthesis metabolism 07_Nucleic acid metabolism 08_Hydrocarbon degradation 09_Carbohydrate Active enzyme - CAZy 10_TCA cycle ... 12_Transporters 13_Hydrogen metabolism 14_Methanogenesis 15_Methylotrophy 16_Embden Meyerhof-Parnos (EMP) 17_Gluconeogenesis 18_Sulfur compounds metabolism 19_Saccharide and derivated synthesis 20_Hydrolysis of polymers 21_Cellular response to stress
date
0.0 0.032555 0.004332 6.551075e-04 0.000551 0.007245 0.050208 0.018190 0.001434 0.007091 0.007711 ... 0.013046 7.636352e-04 0.001359 0.003455 0.009246 0.004036 0.002204 0.015901 0.007996 0.044404
1.0 0.032376 0.004261 1.417759e-20 0.000649 0.007283 0.047614 0.018241 0.001163 0.007493 0.007491 ... 0.012228 1.703635e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016145 0.007861 0.044433
2.0 0.032329 0.004261 1.417756e-20 0.000649 0.007282 0.047304 0.018290 0.001163 0.007542 0.007490 ... 0.012153 1.703597e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016171 0.007860 0.044494
3.0 0.032282 0.004261 1.417798e-20 0.000649 0.007282 0.047108 0.018347 0.001163 0.007596 0.007489 ... 0.012072 1.703636e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016193 0.007859 0.044560
4.0 0.032235 0.004261 1.417867e-20 0.000649 0.007282 0.046958 0.018413 0.001163 0.007650 0.007488 ... 0.011985 1.703717e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016214 0.007858 0.044633
5.0 0.032187 0.004261 1.417960e-20 0.000649 0.007282 0.046824 0.018489 0.001163 0.007695 0.007487 ... 0.011894 1.703833e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016235 0.007857 0.044712
6.0 0.032140 0.004261 1.418084e-20 0.000649 0.007282 0.046689 0.018577 0.001163 0.007726 0.007485 ... 0.011798 1.703990e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016256 0.007856 0.044790
7.0 0.032093 0.004261 1.418264e-20 0.000649 0.007282 0.046514 0.018671 0.001163 0.007735 0.007484 ... 0.011699 1.704220e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016273 0.007854 0.044850
8.0 0.032122 0.004362 8.355870e-04 0.000600 0.007049 0.045215 0.019025 0.001449 0.008429 0.007428 ... 0.011506 6.943123e-04 0.001097 0.003125 0.009361 0.003913 0.002097 0.015956 0.008593 0.045070
9.0 0.031966 0.004261 1.418395e-20 0.000649 0.007283 0.046505 0.018789 0.001163 0.007679 0.007480 ... 0.011494 1.704403e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016354 0.007850 0.044836
10.0 0.031887 0.004261 1.418347e-20 0.000649 0.007284 0.046678 0.018818 0.001163 0.007616 0.007478 ... 0.011390 1.704356e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016421 0.007848 0.044762
11.0 0.031808 0.004261 1.418359e-20 0.000649 0.007284 0.046822 0.018866 0.001163 0.007537 0.007476 ... 0.011286 1.704385e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016494 0.007846 0.044671
12.0 0.031729 0.004261 1.418405e-20 0.000649 0.007286 0.046989 0.018941 0.001163 0.007454 0.007474 ... 0.011183 1.704460e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016584 0.007844 0.044574
13.0 0.031650 0.004261 1.418484e-20 0.000649 0.007287 0.047226 0.019043 0.001163 0.007376 0.007472 ... 0.011082 1.704580e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016709 0.007841 0.044473
14.0 0.031571 0.004261 1.418615e-20 0.000649 0.007288 0.047657 0.019140 0.001163 0.007313 0.007470 ... 0.010982 1.704772e-19 0.001268 0.002820 0.008107 0.003502 0.002264 0.016922 0.007838 0.044353

15 rows × 21 columns

[5]:

from statsmodels.tsa.api import VAR

[6]:

# make VAR model with the imputed data set and statsmodels library
model = VAR(imputed_data)
results = model.fit(maxlags=1, method='ml')

c:\ProgramData\anaconda3\envs\MIMIC\Lib\site-packages\statsmodels\tsa\base\tsa_model.py:473: ValueWarning: An unsupported index was provided and will be ignored when e.g. forecasting.
  self._init_dates(dates, freq)

[7]:

coefficients = results.params
covariance_matrix = results.sigma_u
intercepts = np.array(results.params.iloc[0])

# remove the first row of the coefficients matrix
coefficients = coefficients[1:]
# transpose the coefficients matrix
coefficients = coefficients.T

[8]:

print(coefficients)

                       L1.Acidimicrobium  L1.Acinetobacter  L1.Albidiferax  \
Acidimicrobium                  0.963205         -0.004673       -0.033426
Acinetobacter                  -0.116193          0.909450       -0.122479
Albidiferax                     0.036651         -0.005288        1.025312
Candidatus Microthrix          -0.075924         -0.049265       -0.105313
Chitinophaga pinensis          -0.115842         -0.047209        0.075176
Dechloromonas                   0.014449         -0.000909        0.004961
Haliscomenobacter              -0.007802         -0.004379       -0.045865
Intrasporangium                 0.039053          0.026513        0.021795
Leptospira                      0.165565          0.043335       -0.005578
Other                           0.014019          0.005023        0.029675
Xanthomonas                    -0.027268         -0.002598        0.014894
mean abundance < 2%            -0.010830          0.006473        0.067992

                       L1.Candidatus Microthrix  L1.Chitinophaga pinensis  \
Acidimicrobium                        -0.007765                 -0.003890
Acinetobacter                         -0.053319                 -0.055020
Albidiferax                           -0.010315                 -0.017732
Candidatus Microthrix                  0.945760                 -0.062214
Chitinophaga pinensis                 -0.032266                  0.916255
Dechloromonas                         -0.001062                 -0.000513
Haliscomenobacter                     -0.017300                  0.005880
Intrasporangium                        0.009746                  0.018528
Leptospira                             0.028434                  0.080814
Other                                  0.005560                  0.001574
Xanthomonas                            0.000006                 -0.007796
mean abundance < 2%                    0.007459                  0.002828

                       L1.Dechloromonas  L1.Haliscomenobacter  \
Acidimicrobium                -0.028836             -0.000381
Acinetobacter                 -0.120288             -0.065033
Albidiferax                   -0.010525             -0.007213
Candidatus Microthrix         -0.092386             -0.031745
Chitinophaga pinensis         -0.024099             -0.064282
Dechloromonas                  1.008220             -0.002000
Haliscomenobacter              0.027866              0.972498
Intrasporangium                0.062233              0.011920
Leptospira                     0.040301              0.083109
Other                         -0.006532              0.006801
Xanthomonas                   -0.022118              0.001205
mean abundance < 2%            0.015356             -0.002470

                       L1.Intrasporangium  L1.Leptospira  L1.Other  \
Acidimicrobium                   0.003852      -0.018886 -0.071549
Acinetobacter                   -0.169053      -0.028418  0.082148
Albidiferax                     -0.009145       0.000898 -0.114294
Candidatus Microthrix            0.028549      -0.072750 -0.124845
Chitinophaga pinensis           -0.006870      -0.049551 -0.042289
Dechloromonas                    0.000399       0.001850  0.017999
Haliscomenobacter                0.001219      -0.028812  0.027804
Intrasporangium                  1.013150      -0.001406  0.032484
Leptospira                      -0.013502       1.039789  0.115065
Other                            0.001661       0.010241  0.980034
Xanthomonas                     -0.000700       0.000163 -0.023899
mean abundance < 2%              0.019977       0.026820 -0.100714

                       L1.Xanthomonas  L1.mean abundance < 2%
Acidimicrobium               0.053300               -0.003768
Acinetobacter               -0.351822               -0.037516
Albidiferax                  0.010249               -0.012573
Candidatus Microthrix        0.207496               -0.046151
Chitinophaga pinensis        0.168200               -0.053289
Dechloromonas                0.016044               -0.008142
Haliscomenobacter           -0.088561                0.000027
Intrasporangium              0.056446               -0.010126
Leptospira                  -0.055608               -0.013448
Other                        0.007062                0.004578
Xanthomonas                  0.994634                0.006090
mean abundance < 2%          0.019977                1.019772

[9]:

normalVAR = infer_VAR(data=imputed_data)
normalVAR.debug = 'high'

[10]:

normalVAR.run_inference()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [x0, A, noise_chol]
100.00% [6000/6000 19:48<00:00 Sampling 2 chains, 0 divergences] 
Sampling 2 chains for 1_000 tune and 2_000 draw iterations (2_000 + 4_000 draws total) took 1192 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics

            mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  \
x0[0]      0.535  0.499  -0.364    1.493      0.016    0.012     922.0
x0[1]      1.576  0.941  -0.172    3.329      0.023    0.017    1632.0
x0[2]     -0.098  0.438  -0.867    0.753      0.016    0.011     755.0
x0[3]      1.589  0.890  -0.029    3.303      0.022    0.016    1618.0
x0[4]      2.443  0.760   0.998    3.833      0.024    0.017     988.0
...          ...    ...     ...      ...        ...      ...       ...
A[11, 7]   0.014  0.007  -0.000    0.027      0.000    0.000    1101.0
A[11, 8]   0.021  0.006   0.009    0.032      0.000    0.000    1020.0
A[11, 9]  -0.111  0.023  -0.150   -0.066      0.000    0.000    2425.0
A[11, 10]  0.018  0.021  -0.021    0.058      0.000    0.000    2410.0
A[11, 11]  1.013  0.010   0.994    1.031      0.000    0.000    1281.0

           ess_tail  r_hat
x0[0]        1481.0    1.0
x0[1]        2190.0    1.0
x0[2]        1476.0    1.0
x0[3]        1917.0    1.0
x0[4]        1497.0    1.0
...             ...    ...
A[11, 7]     2244.0    1.0
A[11, 8]     1810.0    1.0
A[11, 9]     2834.0    1.0
A[11, 10]    2720.0    1.0
A[11, 11]    2099.0    1.0

[156 rows x 9 columns]

c:\ProgramData\anaconda3\envs\MIMIC\Lib\site-packages\arviz\plots\plot_utils.py:271: UserWarning: rcParams['plot.max_subplots'] (40) is smaller than the number of variables to plot (156) in plot_posterior, generating only 40 plots
  warnings.warn(

Results saved as:
NetCDF file: model_posterior_default_v1.nc
Data file: data_default_v1.npz
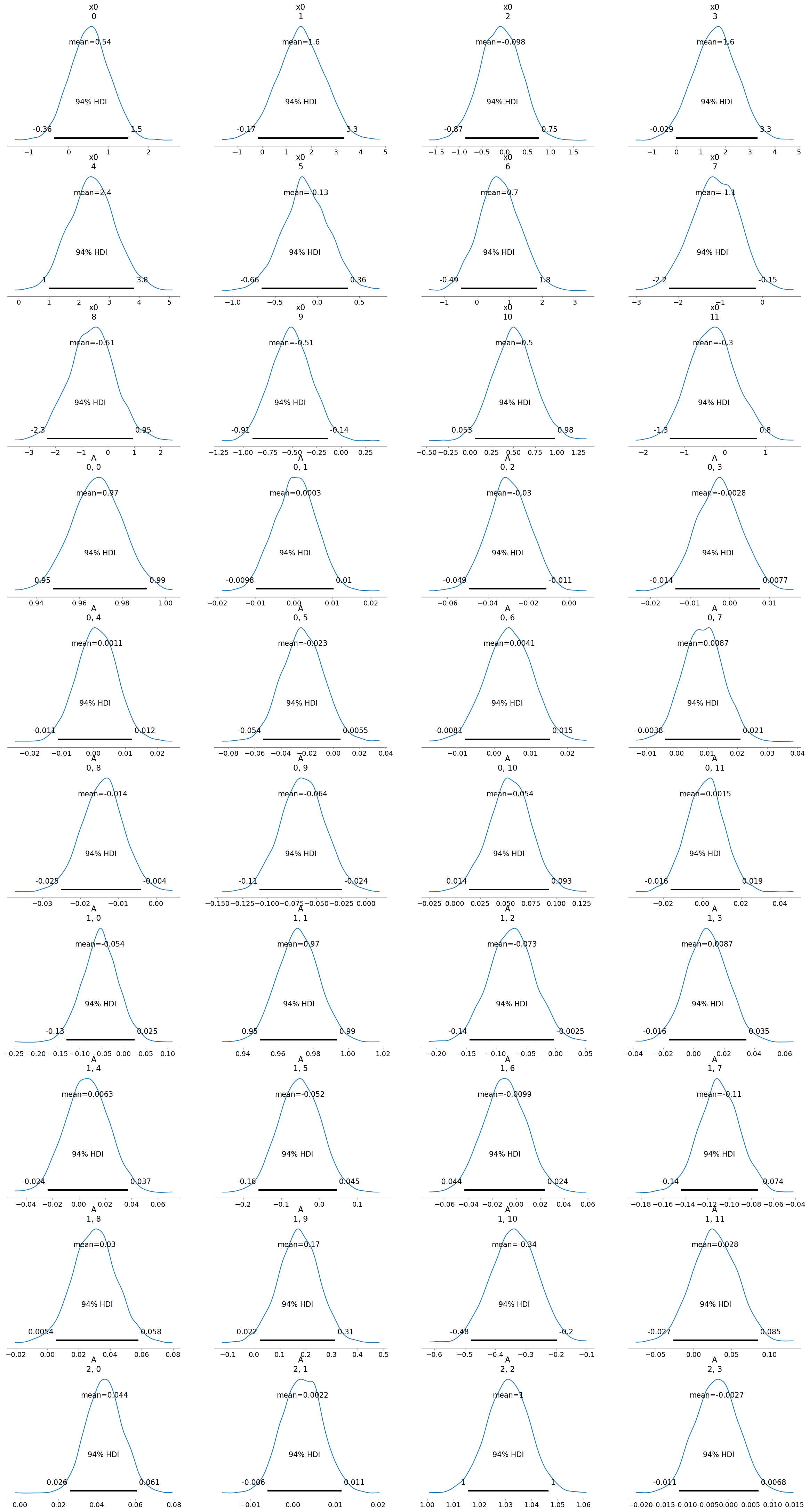
../../../_images/notebooks_MultiModel_Herold_examples-Herold-sVAR_13_6.png 
[11]:

posteriorVAR = az.from_netcdf('model_posterior_default.nc')

[12]:

coefficients = posteriorVAR.posterior['A'].values
coefficients_median = pd.DataFrame(np.median(coefficients, axis=(0, 1)))
intercepts = posteriorVAR.posterior['x0'].values
intercepts_median = np.median(intercepts, axis=(0, 1))

So, these inferences show that there is no easy correlation to infer between the species relative abundances and the metabolite concentrations. This could be due to us trying to infer the causal inference between the relative abundance, and not the change in relative abundance of the species. In the next step, we will try to infer the causal relationships between the change in relative abundance of the species and the metabolite concentrations.

[13]:

# Let's calculate the change in relative abundance for each genus over time from the imputed_data dataset

# Calculate the change in relative abundance for each genus
data_change = imputed_data.diff()

# Make the first row as 0.0 replacing NaN
data_change.iloc[0] = 0.0

[14]:

from statsmodels.tsa.api import VAR

[15]:

# make VAR model with the imputed data set and statsmodels library
model = VAR(data_change)
results = model.fit(maxlags=1, method='ml')

c:\ProgramData\anaconda3\envs\MIMIC\Lib\site-packages\statsmodels\tsa\base\tsa_model.py:473: ValueWarning: An unsupported index was provided and will be ignored when e.g. forecasting.
  self._init_dates(dates, freq)

[16]:

coefficients = results.params
covariance_matrix = results.sigma_u
intercepts = np.array(results.params.iloc[0])

# remove the first row of the coefficients matrix
coefficients = coefficients[1:]
# transpose the coefficients matrix
coefficients = coefficients.T

[17]:

inferChageWithPrior = infer_VAR(data=data_change, dataS=imputed_MP_data,
                                coefficients=coefficients, intercepts=intercepts)
inferChageWithPrior.debug = 'high'

[18]:

inferChageWithPrior.run_inference(method='xs', tune=5000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [X0h, S0h, Ah, Bh, sigma]
100.00% [14000/14000 54:03<00:00 Sampling 2 chains, 2,000 divergences] 
Sampling 2 chains for 5_000 tune and 2_000 draw iterations (10_000 + 4_000 draws total) took 3247 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics

             mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  \
Ah[0, 0]    0.478  0.420   0.058    0.925      0.296    0.251       3.0
Ah[0, 1]    0.008  0.004   0.002    0.016      0.001    0.001      21.0
Ah[0, 2]   -0.191  0.106  -0.297   -0.057      0.074    0.063       3.0
Ah[0, 3]    0.014  0.011   0.005    0.035      0.007    0.005       3.0
Ah[0, 4]   -0.051  0.071  -0.122    0.031      0.050    0.042       3.0
...           ...    ...     ...      ...        ...      ...       ...
Bh[20, 7]   0.179  0.143  -0.164    0.397      0.037    0.027      17.0
Bh[20, 8]  -0.001  0.161  -0.122    0.394      0.095    0.076       3.0
Bh[20, 9]  -0.193  0.657  -1.467    1.257      0.115    0.114      32.0
Bh[20, 10] -0.243  0.404  -0.591    0.515      0.241    0.193       3.0
Bh[20, 11]  0.218  0.177  -0.243    0.501      0.082    0.062       5.0

            ess_tail  r_hat
Ah[0, 0]        32.0   1.94
Ah[0, 1]        31.0   1.87
Ah[0, 2]        41.0   1.84
Ah[0, 3]        21.0   1.90
Ah[0, 4]        21.0   2.06
...              ...    ...
Bh[20, 7]       38.0   1.93
Bh[20, 8]       16.0   2.27
Bh[20, 9]       87.0   1.78
Bh[20, 10]      20.0   2.19
Bh[20, 11]      14.0   1.86

[396 rows x 9 columns]

c:\ProgramData\anaconda3\envs\MIMIC\Lib\site-packages\arviz\plots\plot_utils.py:271: UserWarning: rcParams['plot.max_subplots'] (40) is smaller than the number of variables to plot (396) in plot_posterior, generating only 40 plots
  warnings.warn(

Results saved as:
NetCDF file: model_posterior_xs_v1.nc
Data file: data_xs_v1.npz
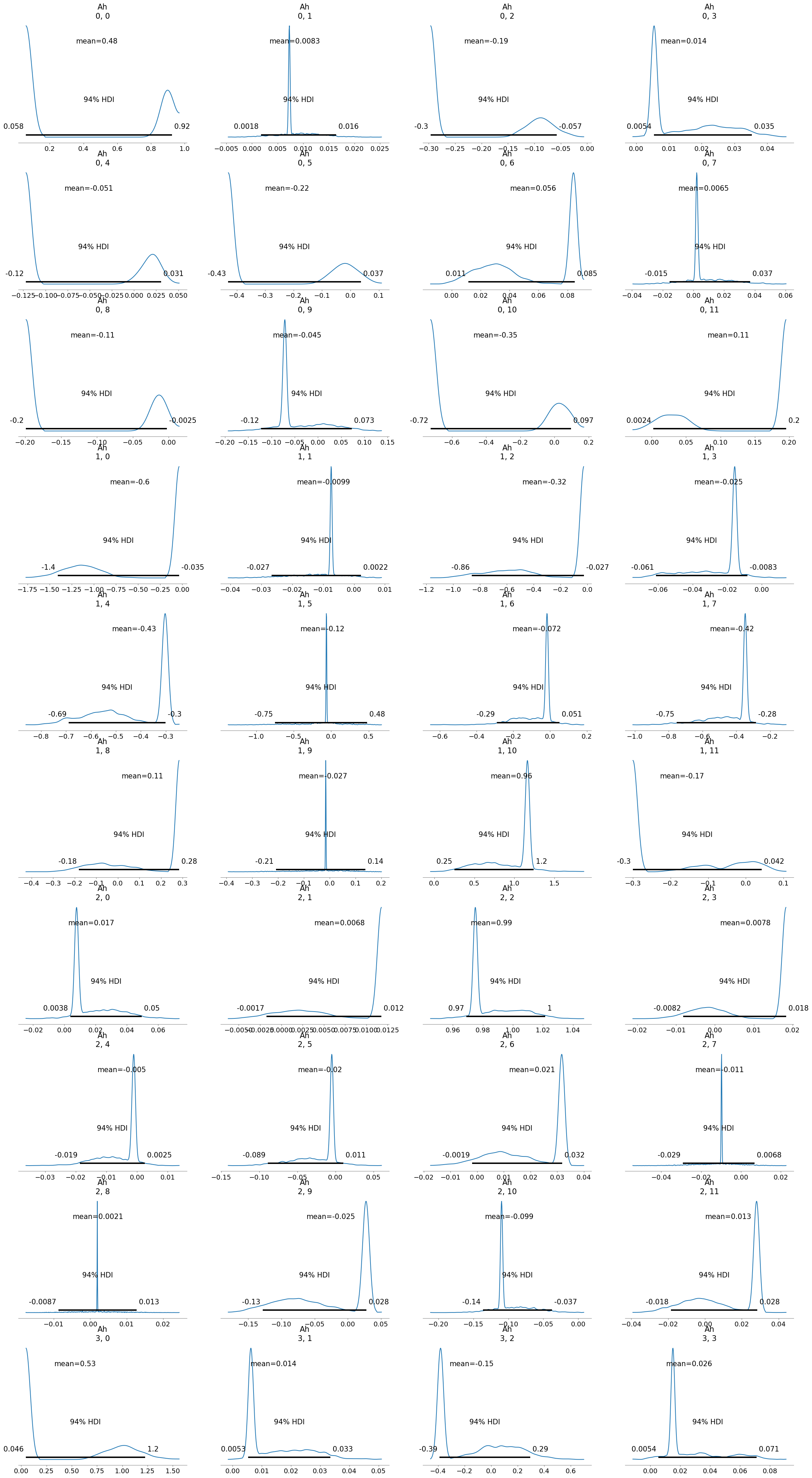
../../../_images/notebooks_MultiModel_Herold_examples-Herold-sVAR_22_6.png 
[19]:

inferChageWithPrior.posterior_analysis()
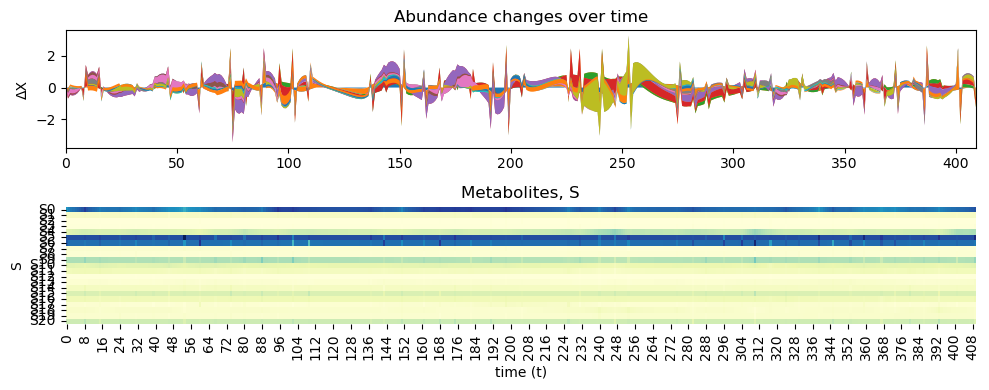
../../../_images/notebooks_MultiModel_Herold_examples-Herold-sVAR_23_0.png
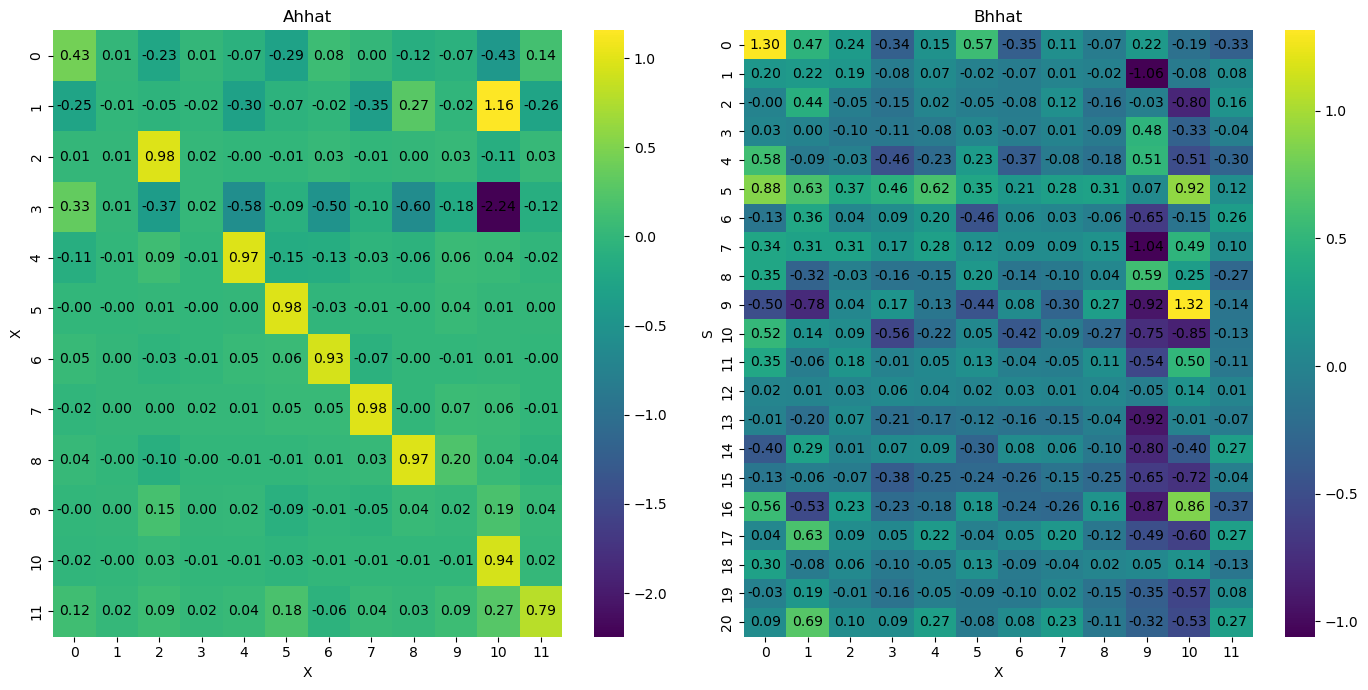
../../../_images/notebooks_MultiModel_Herold_examples-Herold-sVAR_23_1.png

We can also increase the increase the burn-in and number of samples to get more accurate results.

[20]:

inferChageWithPrior2 = infer_VAR(data=data_change, dataS=imputed_MP_data,
                                 coefficients=coefficients, intercepts=intercepts)
inferChageWithPrior2.debug = 'high'

[21]:

inferChageWithPrior2.run_inference(
    method='xs', tune=8000, samples=4000, cores=4)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [X0h, S0h, Ah, Bh, sigma]
100.00% [48000/48000 2:18:51<00:00 Sampling 4 chains, 4,010 divergences] 
Sampling 4 chains for 8_000 tune and 4_000 draw iterations (32_000 + 16_000 draws total) took 8338 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters.  A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
There were 4010 divergences after tuning. Increase `target_accept` or reparameterize.
Chain 0 reached the maximum tree depth. Increase `max_treedepth`, increase `target_accept` or reparameterize.
Chain 1 reached the maximum tree depth. Increase `max_treedepth`, increase `target_accept` or reparameterize.
Chain 2 reached the maximum tree depth. Increase `max_treedepth`, increase `target_accept` or reparameterize.

             mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  \
Ah[0, 0]    0.902  0.019   0.862    0.935      0.002    0.001     199.0
Ah[0, 1]    0.009  0.004   0.002    0.019      0.001    0.000      73.0
Ah[0, 2]   -0.081  0.022  -0.127   -0.047      0.005    0.003      27.0
Ah[0, 3]    0.022  0.007   0.010    0.036      0.001    0.001      52.0
Ah[0, 4]    0.017  0.009   0.002    0.036      0.002    0.001      30.0
...           ...    ...     ...      ...        ...      ...       ...
Bh[20, 7]  -0.022  0.313  -0.515    0.656      0.101    0.074       9.0
Bh[20, 8]   0.063  0.207  -0.400    0.356      0.061    0.044      16.0
Bh[20, 9]  -0.181  0.947  -1.586    1.841      0.207    0.148      24.0
Bh[20, 10]  0.177  0.497  -0.878    0.885      0.125    0.090      15.0
Bh[20, 11]  0.174  0.448  -0.539    0.766      0.181    0.136       6.0

            ess_tail  r_hat
Ah[0, 0]       622.0   1.39
Ah[0, 1]       272.0   1.16
Ah[0, 2]       596.0   1.12
Ah[0, 3]       188.0   1.23
Ah[0, 4]       419.0   1.10
...              ...    ...
Bh[20, 7]       22.0   1.36
Bh[20, 8]       23.0   1.20
Bh[20, 9]      530.0   1.12
Bh[20, 10]      92.0   1.26
Bh[20, 11]      13.0   1.69

[396 rows x 9 columns]

c:\ProgramData\anaconda3\envs\MIMIC\Lib\site-packages\arviz\plots\plot_utils.py:271: UserWarning: rcParams['plot.max_subplots'] (40) is smaller than the number of variables to plot (396) in plot_posterior, generating only 40 plots
  warnings.warn(

Results saved as:
NetCDF file: model_posterior_xs_v2.nc
Data file: data_xs_v2.npz
../../../_images/notebooks_MultiModel_Herold_examples-Herold-sVAR_26_6.png 
[22]:

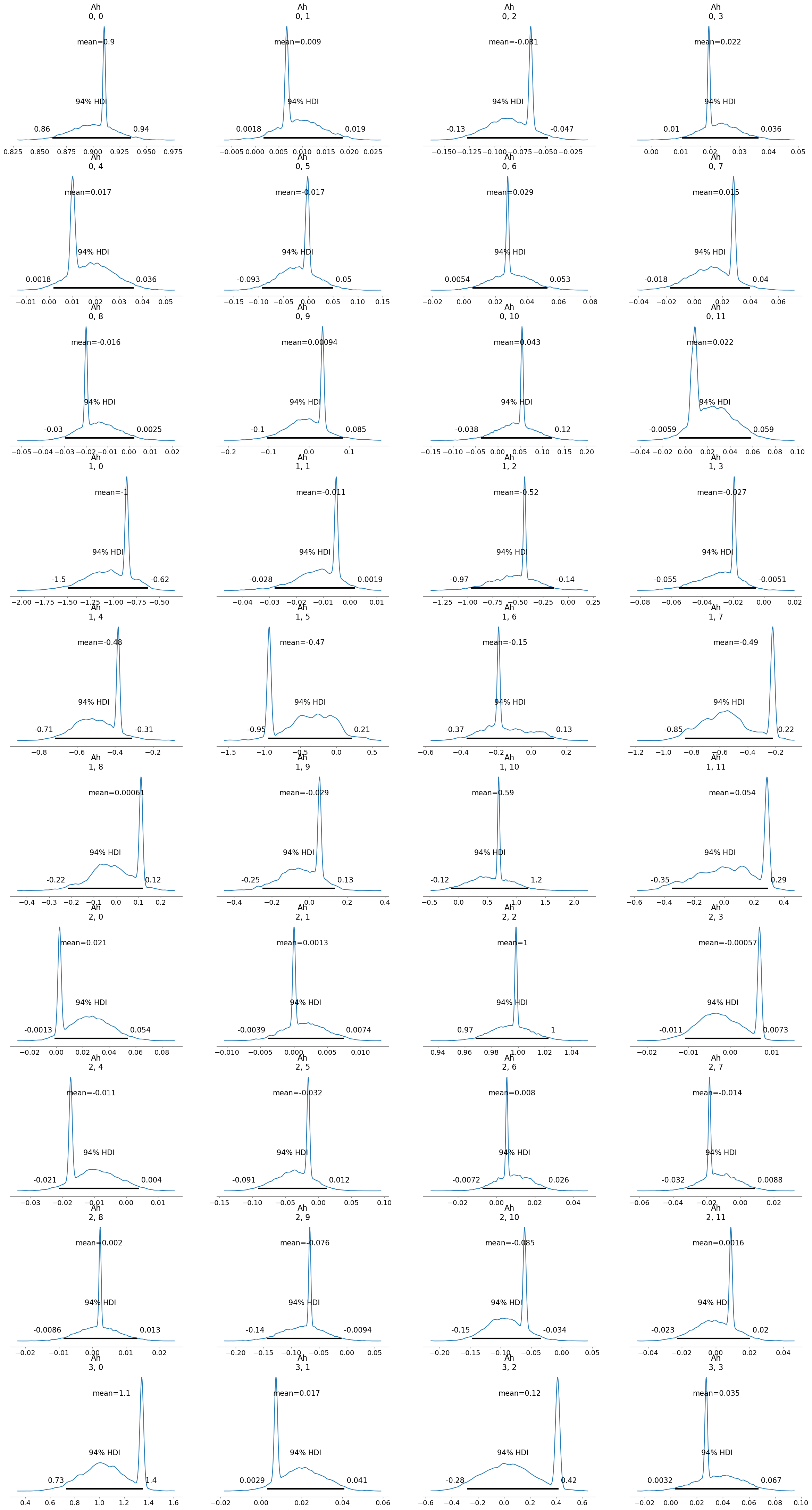
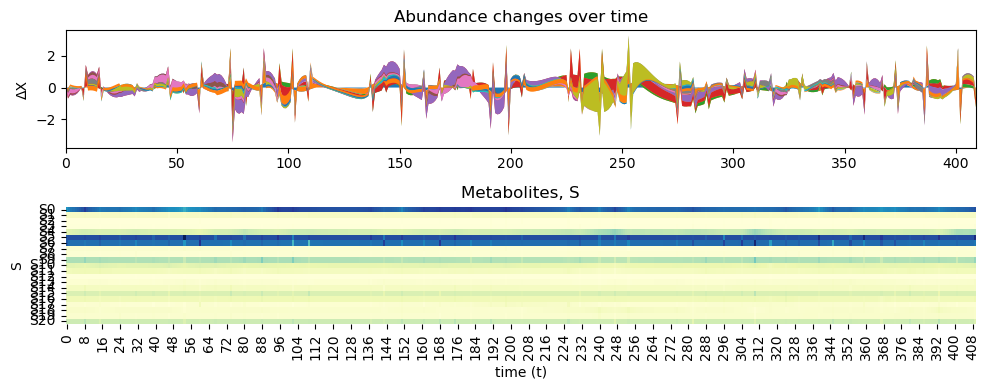
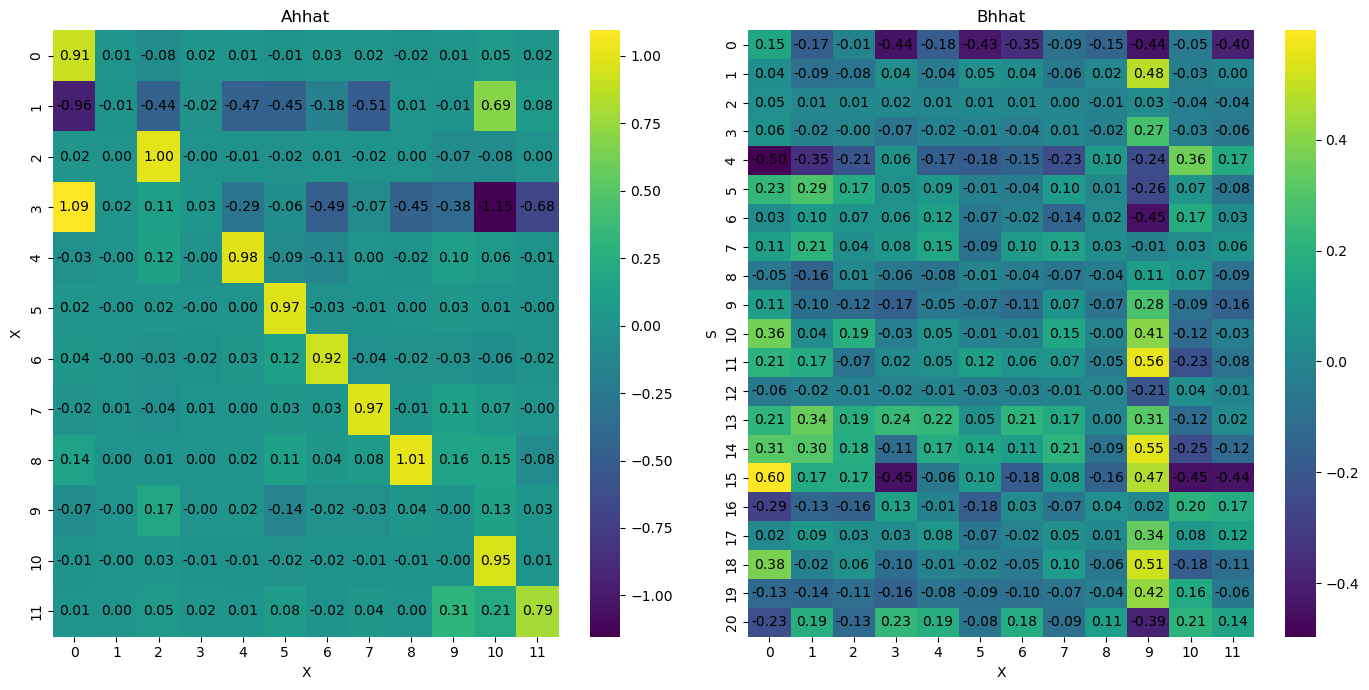
inferChageWithPrior2.posterior_analysis()
../../../_images/notebooks_MultiModel_Herold_examples-Herold-sVAR_27_0.png
../../../_images/notebooks_MultiModel_Herold_examples-Herold-sVAR_27_1.png 
[23]:

# Now we are going to check for stationarity in the data using adf and kpss tests from stasmodels library
# We will use the imputed data set

import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller, kpss


def adf_test(timeseries):
    print("Results of Dickey-Fuller Test:")
    dftest = adfuller(timeseries, autolag="AIC")
    dfoutput = pd.Series(
        dftest[:4],
        index=[
            "Test Statistic",
            "p-value",
            "#Lags Used",
            "Number of Observations Used",
        ],
    )
    for key, value in dftest[4].items():
        dfoutput[f"Critical Value ({key})"] = value
    print(dfoutput)
    # if p-value is less than 0.05, we reject the null hypothesis and say that the data is stationary
    # print if the data is stationary or not
    if dftest[1] <= 0.05:
        print("ADF Test: Data is stationary")
    else:
        print("ADF Test: Data is not stationary")


def kpss_test(timeseries):
    print("Results of KPSS Test:")
    kpsstest = kpss(timeseries, regression="c", nlags="auto")
    kpss_output = pd.Series(
        kpsstest[:3], index=["Test Statistic", "p-value", "Lags Used"]
    )
    for key, value in kpsstest[3].items():
        kpss_output[f"Critical Value ({key})"] = value
    print(kpss_output)
    # if p-value is greater than 0.05, we reject the null hypothesis and say that the data is stationary
    # print if the data is stationary or not
    if kpsstest[1] >= 0.05:
        print("KPSS test: Data is stationary")
    else:
        print("KPSS test: Data is not stationary")

[24]:

# Check for stationarity in the data imputed_dataset (without the 'days' column)
for genus in data_change.columns:
    print(genus)
    adf_test(data_change[genus])
    kpss_test(data_change[genus])
    print("\n")

Acidimicrobium
Results of Dickey-Fuller Test:
Test Statistic                  -4.877743
p-value                          0.000039
#Lags Used                      16.000000
Number of Observations Used    393.000000
Critical Value (1%)             -3.447099
Critical Value (5%)             -2.868923
Critical Value (10%)            -2.570703
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.032404
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Acinetobacter
Results of Dickey-Fuller Test:
Test Statistic                  -4.598946
p-value                          0.000130
#Lags Used                      17.000000
Number of Observations Used    392.000000
Critical Value (1%)             -3.447142
Critical Value (5%)             -2.868941
Critical Value (10%)            -2.570713
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.173686
p-value                   0.100000
Lags Used                10.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Albidiferax
Results of Dickey-Fuller Test:
Test Statistic                  -3.829655
p-value                          0.002618
#Lags Used                      11.000000
Number of Observations Used    398.000000
Critical Value (1%)             -3.446888
Critical Value (5%)             -2.868829
Critical Value (10%)            -2.570653
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.043204
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Candidatus Microthrix
Results of Dickey-Fuller Test:
Test Statistic                -7.937074e+00
p-value                        3.391025e-12
#Lags Used                     6.000000e+00
Number of Observations Used    4.030000e+02
Critical Value (1%)           -3.446681e+00
Critical Value (5%)           -2.868739e+00
Critical Value (10%)          -2.570605e+00
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.094575
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Chitinophaga pinensis
Results of Dickey-Fuller Test:
Test Statistic                  -3.816479
p-value                          0.002743
#Lags Used                      16.000000
Number of Observations Used    393.000000
Critical Value (1%)             -3.447099
Critical Value (5%)             -2.868923
Critical Value (10%)            -2.570703
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.059832
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Dechloromonas
Results of Dickey-Fuller Test:
Test Statistic                  -3.320016
p-value                          0.014007
#Lags Used                      15.000000
Number of Observations Used    394.000000
Critical Value (1%)             -3.447057
Critical Value (5%)             -2.868904
Critical Value (10%)            -2.570693
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.106131
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Haliscomenobacter
Results of Dickey-Fuller Test:
Test Statistic                  -3.790187
p-value                          0.003009
#Lags Used                      17.000000
Number of Observations Used    392.000000
Critical Value (1%)             -3.447142
Critical Value (5%)             -2.868941
Critical Value (10%)            -2.570713
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.099982
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Intrasporangium
Results of Dickey-Fuller Test:
Test Statistic                  -4.249279
p-value                          0.000543
#Lags Used                      18.000000
Number of Observations Used    391.000000
Critical Value (1%)             -3.447186
Critical Value (5%)             -2.868960
Critical Value (10%)            -2.570723
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.197429
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Leptospira
Results of Dickey-Fuller Test:
Test Statistic                  -3.825629
p-value                          0.002656
#Lags Used                      17.000000
Number of Observations Used    392.000000
Critical Value (1%)             -3.447142
Critical Value (5%)             -2.868941
Critical Value (10%)            -2.570713
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.039661
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Other
Results of Dickey-Fuller Test:
Test Statistic                -7.502466e+00
p-value                        4.218178e-11
#Lags Used                     6.000000e+00
Number of Observations Used    4.030000e+02
Critical Value (1%)           -3.446681e+00
Critical Value (5%)           -2.868739e+00
Critical Value (10%)          -2.570605e+00
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.075135
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary


Xanthomonas
Results of Dickey-Fuller Test:
Test Statistic                  -3.684859
p-value                          0.004331
#Lags Used                      18.000000
Number of Observations Used    391.000000
Critical Value (1%)             -3.447186
Critical Value (5%)             -2.868960
Critical Value (10%)            -2.570723
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.1455
p-value                   0.1000
Lags Used                11.0000
Critical Value (10%)      0.3470
Critical Value (5%)       0.4630
Critical Value (2.5%)     0.5740
Critical Value (1%)       0.7390
dtype: float64
KPSS test: Data is stationary


mean abundance < 2%
Results of Dickey-Fuller Test:
Test Statistic                  -4.761013
p-value                          0.000065
#Lags Used                       7.000000
Number of Observations Used    402.000000
Critical Value (1%)             -3.446722
Critical Value (5%)             -2.868757
Critical Value (10%)            -2.570614
dtype: float64
ADF Test: Data is stationary
Results of KPSS Test:
Test Statistic            0.189282
p-value                   0.100000
Lags Used                11.000000
Critical Value (10%)      0.347000
Critical Value (5%)       0.463000
Critical Value (2.5%)     0.574000
Critical Value (1%)       0.739000
dtype: float64
KPSS test: Data is stationary



C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")
C:\Users\User\AppData\Local\Temp\ipykernel_16772\3039934652.py:33: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")

[25]:

import numpy as np

[26]:

posteriorVAR = az.from_netcdf('model_posterior_xs_v2.nc')

posterior_samples = posteriorVAR.posterior['Ah'].values

[27]:

# Compute the median of the posterior samples
median_Ah = np.median(posterior_samples, axis=(0, 1))

[28]:

# Function to check stability of a single matrix
def is_stable(matrix):
    eigenvalues = np.linalg.eigvals(matrix)
    # return all(np.sqrt(np.real(eigenvalue)**2 + np.imag(eigenvalue)**2) < 1 for eigenvalue in eigenvalues)
    return np.all(np.abs(eigenvalues) < 1)


# Check stability of the median matrix
stability_median_Ah = is_stable(median_Ah)

print("Median Ah matrix stability:", stability_median_Ah)
if stability_median_Ah:
    print("The median Ah matrix is stable.")
else:
    print("The median Ah matrix is not stable.")

Median Ah matrix stability: True
The median Ah matrix is stable.

[29]:

# Function to check stability of a single matrix
def is_stable(matrix):
    eigenvalues = np.linalg.eigvals(matrix)
    return np.all(np.abs(eigenvalues) < 1)


# Check stability for each sampled matrix
num_chains, num_samples, nX, _ = posterior_samples.shape
stability_results = np.zeros((num_chains, num_samples))

for chain in range(num_chains):
    for sample in range(num_samples):
        stability_results[chain, sample] = is_stable(
            posterior_samples[chain, sample])

# Percentage of stable samples
stable_percentage = np.mean(stability_results) * 100
print(f"Percentage of stable samples: {stable_percentage:.2f}%")

if stable_percentage < 100:
    print("Warning: Not all samples are stable.")
else:
    print("All samples are stable.")

Percentage of stable samples: 87.48%
Warning: Not all samples are stable.