[1]:
from mimic.utilities.utilities import set_all_seeds
from mimic.utilities.utilities import plot_gMLV
from mimic.model_infer import *
from mimic.model_simulate import *
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
Simulate some time course data from the gMLV¶
The generalized Lotka-Volterra equation takes the form
where:
\(X_i\) is the concentration of a species
\(\mu_i\) is its specific growth rate
\(M_{ij}\) is the effect of the interaction of species \(i\) on species \(j\)
\(\epsilon_{il}\) is the susceptibility to the time-dependent perturbation \(u_l\)
here we add metabolites to the model as in Clark et al., 2021: eqs(4 & 5)
where:
\(S_k\) is the concentration of a metabolite, \(k\)
\(A_{ki}\) is the productivity of metabolite \(k\), due to species \(i\)
Notes
This model assumes metabolite production is associated with abundance: dS/dt ~ X. Some models assume dS/dt ~ dX/dt which means production is related to growth
This model is poorly defined as it can run in to problems with negative productivities
There is no influence of S on X, which can be modified in future
Five species, six metabolites, single time course¶
[2]:
# Simulate some microbiota and metabolites
set_all_seeds(1234)
# SETUP MODEL
# establish size of model
num_species = 5
num_metabolites = 6
# construct interaction matrix
# TODO do this programmatically
M = np.zeros((num_species, num_species))
np.fill_diagonal(M, [-0.05, -0.1, -0.15, -0.01, -0.2])
# M[0,2] = -0.025
M[1, 3] = 0.05
# M[4,0] = 0.02
# construct growth rates matrix
mu = np.random.lognormal(0.01, 0.5, num_species)
# construct metabolite production matrix
alpha = np.zeros((num_metabolites, num_species))
alpha[1, 4] = 1
alpha[4, 2] = -0.5
# instantiate simulator
simulator = sim_gMLV(num_species=num_species,
num_metabolites=num_metabolites,
M=M,
mu=mu,
beta=alpha)
# simulator.print()
# PRODUCE SIMULATED RESULTS
# initial conditions
init_species = 10 * np.ones(num_species)
init_metabolites = 10 * np.ones(num_metabolites)
times = np.arange(0, 5, 0.1)
yobs, sobs, sy0, _, _, _ = simulator.simulate(
times=times, sy0=np.hstack((init_species, init_metabolites)))
# add some gaussian noise
yobs = yobs + np.random.normal(loc=0, scale=0.1, size=yobs.shape)
sobs = sobs + np.random.normal(loc=0, scale=0.1, size=sobs.shape)
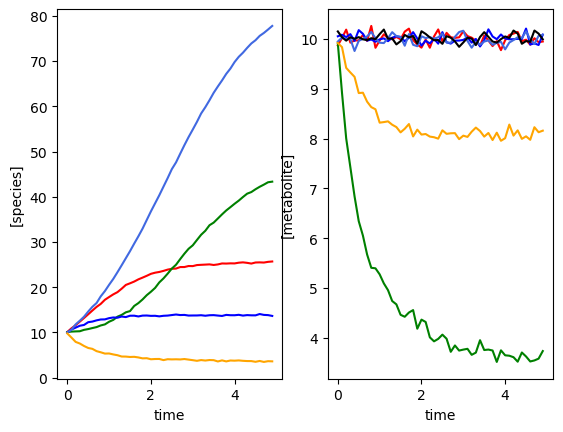
# plot simulation
plot_gMLV(yobs, sobs, times)
Using the following parameters for gMLV simulation: {'num_species': 5, 'num_metabolites': 6, 'num_perturbations': 0, 'mu': array([1.27853844, 0.55683415, 2.06752757, 0.86387608, 0.70448068]), 'M': array([[-0.05, 0. , 0. , 0. , 0. ],
[ 0. , -0.1 , 0. , 0.05, 0. ],
[ 0. , 0. , -0.15, 0. , 0. ],
[ 0. , 0. , 0. , -0.01, 0. ],
[ 0. , 0. , 0. , 0. , -0.2 ]]), 'beta': array([[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. , 1. ],
[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0. , -0.5, 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. ]]), 'epsilon': array([], shape=(5, 0), dtype=float64)}
[3]:
simulator.print_parameters()
Model parameters:
Model: gMLV
num_species: 5
num_metabolites: 6
num_perturbations: 0
mu: [1.28 0.56 2.07 0.86 0.7 ]
M: [[-0.05 0. 0. 0. 0. ]
[ 0. -0.1 0. 0.05 0. ]
[ 0. 0. -0.15 0. 0. ]
[ 0. 0. 0. -0.01 0. ]
[ 0. 0. 0. 0. -0.2 ]]
beta: [[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 1. ]
[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. ]
[ 0. 0. -0.5 0. 0. ]
[ 0. 0. 0. 0. 0. ]]
epsilon: []
[5]:
simulator.read_parameters("simulator_parameters.json")
simulator.print_parameters()
Model parameters:
Model: gMLV
num_species: 5
num_metabolites: 6
num_perturbations: 0
mu: [1.28 0.56 2.07 0.86 0.7 ]
M: [[-0.05 0. 0. 0. 0. ]
[ 0. -0.1 0. 0.05 0. ]
[ 0. 0. -0.15 0. 0. ]
[ 0. 0. 0. -0.01 0. ]
[ 0. 0. 0. 0. -0.2 ]]
beta: [[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 1. ]
[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. ]
[ 0. 0. -0.5 0. 0. ]
[ 0. 0. 0. 0. 0. ]]
epsilon: []
Five species, single time course, with a perturbation¶
[6]:
set_all_seeds(1234)
# SETUP MODEL
# establish size of model
num_species = 5
num_metabolites = 0
# construct interaction matrix
# TODO #49 do this programmatically
M = np.zeros((num_species, num_species))
np.fill_diagonal(M, [-0.05, -0.1, -0.15, -0.01, -0.2])
M[0, 2] = -0.025
M[1, 3] = 0.05
M[4, 0] = 0.02
# construct growth rates matrix
mu = np.random.lognormal(0.01, 0.5, num_species)
# construct perturbation matrix
npert = 1
epsilon = np.zeros([num_species, npert])
epsilon[:, 0] = [0, -1, 0, -1, 0]
# instantiate simulator
simulator = sim_gMLV(num_species=num_species,
num_metabolites=num_metabolites,
num_perturbations=npert,
M=M,
mu=mu,
epsilon=epsilon)
simulator.print_parameters()
# PRODUCE SIMULATED RESULTS
# initial conditions
init_species = 10 * np.ones(num_species)
init_metabolites = 10 * np.ones(num_metabolites)
# perturbation information encoded in a function
def pert_fn(t):
return np.array([1]) if 2.0 <= t < 2.2 else np.array([0])
times = np.arange(0, 5, 0.1)
yobs, sobs, sy0, mu, M, _ = simulator.simulate(times=times,
sy0=np.hstack(
(init_species, init_metabolites)),
u=pert_fn)
# add some gaussian noise
yobs = yobs + np.random.normal(loc=0, scale=0.1, size=yobs.shape)
sobs = sobs + np.random.normal(loc=0, scale=0.1, size=sobs.shape)
# plot simulation
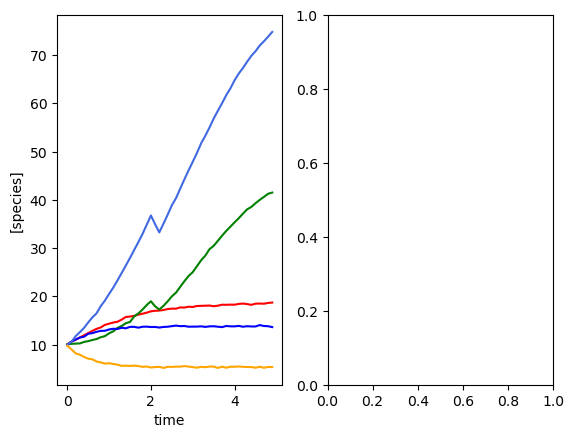
plot_gMLV(yobs, sobs, times)
Model parameters:
Model: gMLV
num_species: 5
num_metabolites: 0
num_perturbations: 1
mu: [1.28 0.56 2.07 0.86 0.7 ]
M: [[-0.05 0. -0.03 0. 0. ]
[ 0. -0.1 0. 0.05 0. ]
[ 0. 0. -0.15 0. 0. ]
[ 0. 0. 0. -0.01 0. ]
[ 0.02 0. 0. 0. -0.2 ]]
beta: None
epsilon: [[ 0.]
[-1.]
[ 0.]
[-1.]
[ 0.]]
Warning: Missing or None parameters for gMLV simulation. Using default values for: ['beta']
Using the following parameters for gMLV simulation: {'num_species': 5, 'num_metabolites': 0, 'num_perturbations': 1, 'mu': array([1.27853844, 0.55683415, 2.06752757, 0.86387608, 0.70448068]), 'M': array([[-0.05 , 0. , -0.025, 0. , 0. ],
[ 0. , -0.1 , 0. , 0.05 , 0. ],
[ 0. , 0. , -0.15 , 0. , 0. ],
[ 0. , 0. , 0. , -0.01 , 0. ],
[ 0.02 , 0. , 0. , 0. , -0.2 ]]), 'beta': None, 'epsilon': array([[ 0.],
[-1.],
[ 0.],
[-1.],
[ 0.]])}